미분방정식(5)
2012년 12월 10일 월요일
오전 4:17

ㅋㅋㅋ 돌아왔슴돠~
시험결과는 안습입니다. ㅜ.ㅜ
묻지 마세요~!
그럼 진도 들어가서~~
저희 401페이지 예제3까지 했었어요
그러니 오늘은 예제4를 해야해요
바로 갑니다~
예제4. 원점과 점 ( ln 2 , 3/4 )를 지나는 y''=y의 해를 구하여라.
일단, 이런 형태의 미방을 풀었을 때
해가 익스포넨셜로 나온다는 것은 미분방정식(4) 를 참고해 주세요~!
솔직히 복잡하게 생각 할 필요도 없이
두 번 미분해서 자기 자신이 나오는 함수!
대표적인 함수가 익스포넨셜 함수 아니겠어요?
그런데...


그럼 일반해는 무엇일까요?
그리고 선형 미방에서 일반해는 특수해의 합으로 표현 가능한데...
좀 어렵게 표현하면
선형 미분방정식의 일반해는 가능한 해들의 선형결합으로 구할 수 있다.
라고 할 수 있습니다.
이 부분은 설명이 너무 부족하고
제가 잘못 전달한 내용이라서 오개념 소지가 많아 삭제하고,
다음 기회에 일반해를 구하는 방법에 대해 더 깊이 다루겠습니다.
일단 위키피디아 상미분방정식에서 발췌 한 표를 참고 해 주세요!
| case | 근 | 기저 | 일반해 |
|---|---|---|---|
 | 서로 다른 실근  |  |  |
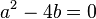 | 실이중근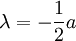 | 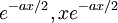 |  |
 | 공액복소수 |  |  |
현재 일반해와 특수해에 대한
포스팅이 완료되었습니다.
6강부터 보시고 오세요~^^
물론 이 정의는 비선형에서는 맞지 않습니다.
왜인지는... 오늘 이 글을 읽으면 조금만 생각하면 답이 나오실 겁니다.
지금 우리가 풀려고 하는 미분방정식은 선형이죠?
선형미방의 정의를 까먹으셨다면
여기를 클릭하셔서 보고오세요~^^
그리고 서비스로 다른 설명도 첨부하면

이 식을 보면 "두번 미분"="자기자신" 이죠?
그런데 미분 한다는 것은
"주어진 함수에 미분연산자를 적용한 것"
입니다.
그리고 연산자를 적용한다는 것은
"주어진 관찰대상의 상태에서 원하는 물리량을 꺼내는 행위"
라고 송중기 예를 들어서 이야기 했었죠?
일상적인 예를 들면
송중기의 몸무게를 알고 싶다.
이게 계산 목적입니다.
그리고 송중기를 저울에 올린다.
이게 함수에 적당한 연산자를 적용해서 식을 만드는 겁니다.
송중기의 몸무게가 65kg이라는 것을 관측한다.
이건 함수에 연산자를 적용시켜 계산하면 튀어나오는 값에 매치됩니다.
이 개념은 양자역학에서 비로소 빛을 발하는데...
간만 볼 정도로 간단히 예를 들고 넘어가겠습니다.
파동함수에 해밀토니안 연산자를 적용하면 에너지 값이 나온다.
위의 말을 수식으로 표현하면 다음과 같이 표기하는데

위 수식을 수학적으로 말하면, 헤밀토니안 연산자는 관측대상의 상태를 선형변환 시키는 연산자이고, 이때 관측대상의 상태는 고유벡터이고, 연산을 하고 나오는 고유값이 의미하는 물리량이 바로 에너지 이다.
라는 의미 입니다.
여기서 제가 말하고 싶은 것은
송중기를 저울 위에 올려놓는다고 송중기가 갑자기 노홍철이 되나요?
송중기는 저울 위에 올라가도 여전히 잘생겼습니다!
홍철형님은...에효... ㅋㅋㅋ

축하해요 F1
아 또 말이 샜네 ㅋㅋㅋㅋㅋㅋㅋㅋ
암튼 연산자를 적용 해도 원래 함수의 상태는 바뀌지 않는 것!
다시 말해
"원하는 관측량을 관측해도 관찰대상의 본래 상태는 변하지 않는 것!"
물리에서는 이런 상황이 매우 많기 때문에 선형미분방정식을 풀 일이 많은 것 입니다.
그리고 관측 대상의 상태는 관측한 물리량의 선형결합으로 구할 수 있고
이 때,
특수한 조건 하에서 관측 대상을 관측한 물리량과 그 상태= 특수해
관측대상이 가질 수 있는 가능성이 있는 상태 = 일반해
이렇게 매치 시킬 수 있습니다.
그래서 선형미분방정식의 일반해는
여러 가지 특수해들의 합으로 표현 할 수 있다는 것이고...


그리고 문제를 다시 가져와 보면
예제4. 원점과 점 ( ln 2 , 3/4 )를 지나는 y''=y의 해를 구하여라.
y가 갖춰야 할 조건이 나오는데...
이걸 만족시키는 형태를 찾는 것은 매우 쉽습니다.
그냥 대입하면 되거든요~
일단 원점부터 대입 해 볼까요?


이런 결과가 나옵니다.




문제에서 주어진 조건을 만족하는 해는

마지막에 하이퍼볼릭사인함수가 나온 이유는... 정의입니다.
쌍곡선함수를 참고해 주세요
연애를 할 때도 이렇게 생각해서 들어가잖아요?
난 게이가 아니니깐 연애는 여자랑 해야지!
라고 생각하면 일반해=여성
이렇게 되는 것이고...
여기에 갖가지 초기조건과 경계조건을 적용하면
초기조건 1 : 한국 국적으로 내어남.
경계조건 1 : 예쁘다.
경계조건 2 : 착하다.
경계조건 3 : 미성년자가 아니다.
.
.
.
.
이런 여러 경계조건 만족하는 특수해=우리 여보님~♥♥♥♥♥♥♥
이렇게 되는 것이지요~ㅋㅋ
네! 저 솔로 아녜요!
커플임 ㅋㅋㅋ
근데 한국-캐나다에 있는 기러기 커플인건 안자랑 ㅜ.ㅜ
암튼 실험실에서 관측을 원하는 물리량 이외의 변수들을 고정시켜놓고 실험하는 경우가 많기도 하고... 물질 고유의 특성이라는 것이 존재하기 때문에 이렇게 몇 가지 주어진 조건을 수학적으로 만족시켜야 할 필요가 있습니다.
이런 조건을 경계조건, 초기조건이라고 합니다.
아직은 초반이라 이런저런 부가설명이 많아서 진도도 별로 못나가고 있는데...
언젠가 진도 팍팍 나갈 수 있는 날이 오겠죠?
이제 곧 새해인데...
내년에 공부 시작하는 우리 후배님들을 위해서
최대한 진도 뽑아보겠습니다~!!
그리고...
보시고 그냥 가시지 마시고
좋으면 좋다고 손가락도 눌러 주시고
광고도 클릭 해 주셔서 제 살림이 보탬도 좀 되어 주시고...
블로그도 많이 많이 놀러 와 주세요~~^^
무엇보다 댓글좀... ^^;
이게 몰랐는데 하다 보니깐 댓글 하나하나가 큰 힘이 되더라고요
혼자서 이런 고생 하는 것이 기특하지 않나요? ㅋㅋ
힘좀 주세요~~^^
Microsoft OneNote 2010을(를) 사용하여 작성했습니다.
모든 노트 및 정보를 한 곳에서 볼 수 있습니다.
'물리학 > 수리물리' 카테고리의 다른 글
| 8강. 일반해와 특수해(4) (2) | 2012.12.23 |
|---|---|
| 7강. 일반해와 특수해(3) (6) | 2012.12.23 |
| 6강. 일반해와 특수해(2) (10) | 2012.12.22 |
| 4강. 미분방정식의 해는 exponential? (15) | 2012.11.13 |
| 3강. 미분방정식 (6) | 2012.11.09 |
| 2강. 선형이 찾았다~~ㅋㅋ(송중기 개객끼) (1) | 2012.11.07 |
| 1강. 선형이를 찾습니다. (2) | 2012.11.05 |




